WebGL中的数学：模型矩阵、视图矩阵和投影矩阵

WebGL（Web Graphics Library）是一种用于在Web浏览器中绘制3D图形的技术。在WebGL中，数学是不可或缺的一部分，涉及坐标变换、角度与弧度转换、矩阵运算以及法向量变换等，三种矩阵合并称之为MVP。

1. 模型矩阵（Model Matrix）

模型矩阵用于将物体从世界坐标系变换到相机坐标系。它定义了如何在3D世界空间中平移、旋转和缩放原始模型数据。通常，我们将模型矩阵与物体的顶点坐标相乘，以实现模型的变换。

// 示例：创建一个平移的模型矩阵

const translationMatrix = mat4.create();
mat4.translate(translationMatrix, translationMatrix, [x, y, z]);

1.1 平移矩阵

一个点的坐标是(x,y,z),假设沿着X、Y、Z轴分别平移Tx、Ty、Tz，毫无疑问平移后的坐标是(x+Tx,y+Ty,z+Tz)。

坐标是(x,y,z)转化为齐次坐标坐标是(x,y,z,1),可以用4x1矩阵表示，这种特殊形式，也可以称为列向量，在webgpu顶点着色器代码中也可以用四维向量vec4表示。

1.2 缩放矩阵

通过缩放矩阵可以对顶点的齐次坐标进行缩放。

1.3 旋转矩阵

• 绕Z轴旋转α角度

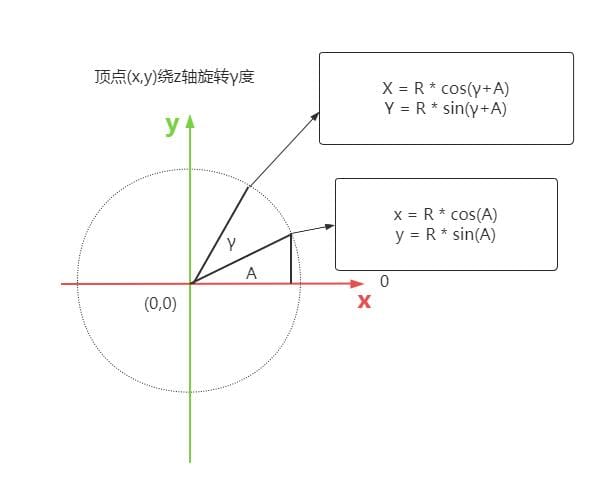
旋转后的坐标：X=xcosγ-ysinγ,Y=xsinγ+ycosγ

• 绕X轴旋转α角度

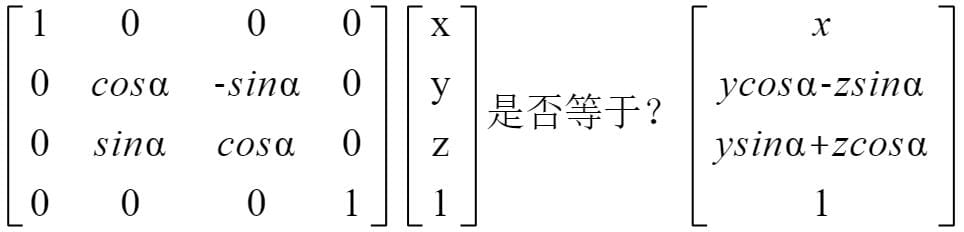
x的坐标不变，y、z的坐标发生变化，Y=ycosα-zsinα,Z=ysinα+zcosα

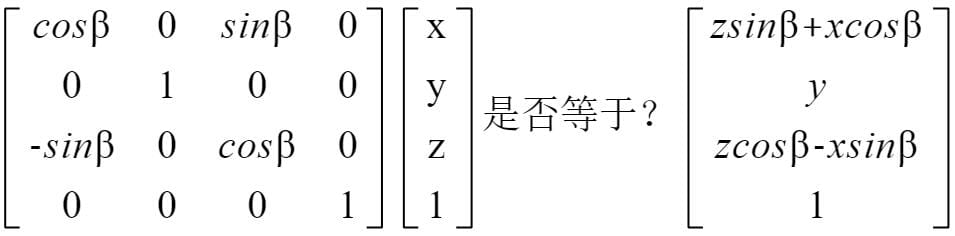
• 绕Y轴旋转β角度

y的坐标不变，z、x的坐标发生变化，Z=zsinβ+xcosβ,X=zcosβ-xsinβ

2. 视图矩阵（View Matrix）

视图矩阵用于模拟相机的位置和方向。它将物体从相机坐标系变换到裁剪坐标系。视图矩阵通常包括平移、旋转和缩放操作，以模拟相机的移动和观察方向。

// 示例：创建一个相机位置的视图矩阵

const viewMatrix = mat4.create();
mat4.lookAt(viewMatrix, [eyeX, eyeY, eyeZ], [targetX, targetY, targetZ], [upX, upY, upZ]);

3. 投影矩阵（Projection Matrix）

投影矩阵用于将相机坐标系中的坐标变换到裁剪坐标系。不同类型的投影矩阵（如透视投影和正交投影）可以模拟不同相机的效果。

// 示例：创建一个透视投影矩阵

const projectionMatrix = mat4.create();
mat4.perspective(projectionMatrix, fov, aspectRatio, near, far);

4. 组合使用

模型、视图和投影矩阵在渲染3D场景时，通常将模型矩阵、视图矩阵和投影矩阵组合在一起，以便将顶点从模型空间变换到裁剪空间。

// 示例：组合模型、视图和投影矩阵

const mvpMatrix = mat4.create();
mat4.multiply(mvpMatrix, projectionMatrix, viewMatrix);
mat4.multiply(mvpMatrix, mvpMatrix, modelMatrix);